导语

赌王何鸿燊接手葡京赌场时，业务蒸蒸日上，但理性的赌王仍然忐忑，请教“赌神”叶汉：“如果这些赌客总是输，长此以往，他们不来了怎么办？”叶汉笑道：“一次赌徒，一世赌徒，他们担心的是赌场不在怎么办。”

叶汉说的只是心理层面，现代赌场程序方面的设计，比叶汉当年要缜密得多。

赌徒永远不明白，与自己对赌的不是运气，也不是庄家，他们是在与狄利克雷、伯努利、高斯、纳什、凯利这样的大师对决数学，赢的胜率能有多大？

在投资圈被封为“资金管理神器”的凯利公式有个最基本的道理：正期望值的游戏才可以下注。

正如芒格所说：“当世界给予你机会的时候，聪明的投资者会出重手。当他们具有极大赢面时，他们会下大注。其余的时间里，他们做的仅仅是等待。”

远离赌博，谨慎投资，尽量别投机，去做正期望值的事情。

以下，祝开卷有得。

01

首先，我们要区分一下：

投资、投机、赌博之间，到底有什么区别？

看起来，这三者都充满了不确定性。

企业家和投资家们，也经常喜欢说：让我们赌一把吧。

说起来，好像都是为看不见的未来下注：

赌赢了就是投资成功；

赢得惊险赚得很多就是投机成功；

失败了便被视为“赌输了”。

人生一场，谁不是赌呢？

这种想法，其实是不思进取、不动脑子的自暴自弃。

为了避免掉入毫无意义的讲大道理和文字游戏，在这里，我想用一个简单粗暴的方式来定义：

期望值未知的，是投机。

有投资经验的客官可能会说了，你这不是废话吗？既然说了是不确定性，就很难分清期望值是正是负。要是知道期望值，谁不会赚钱啊？

果真如此吗？

未必。

本文的前几部分看起来很简单。不过，现实中，我们犯的绝大多数错误，都出现在简单的常识方面。

我将事件的不确定性、时间的不确定性和筹码的不确定性整合在一起，去探寻如何用概率思维来构建一个体系。

何妨一起重温一下？

02

期望值的概念虽然非常简单，但真正能搞明白的，没多少人，在人群中也许小于1%。

曾翻过一本据说卖了几十万册的畅销书，里面有一节讲概率，作者居然混淆了概率、赔率、期望值等基本概念。

让我们从头复习一下期望值：

在概率论和统计学中，一个离散性随机变量的期望值（或数学期望，亦简称期望，物理学中称为期待值）是试验中每次可能的结果乘以其结果概率的总和。

换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。

举个例子，你一直扔一个骰子很多很多次，你得到每一个的可能性是一样的，那么你扔一个骰子的期望值就是：

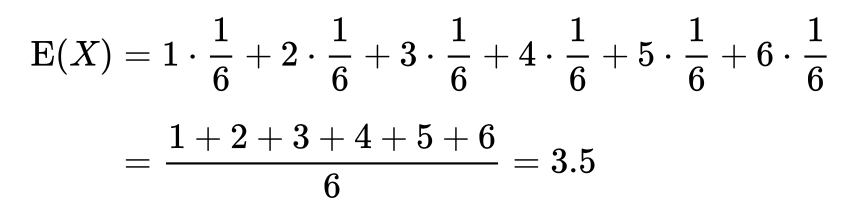
那么，由此可以计算得出，掷一枚公平的六面骰子，其每次“点数”的期望值是3.5。

这是无限多次重复后，得到的一个平均值。

03

这么简单的一个框架，是几乎所有投资高手必备的第一公式。

鲁宾举过一个高盛的投资套利的案例：

有一次，在某两家公司宣布合并之后，高盛打算做一次套利。

尽管宣布了消息，但是该合并可能成功，也可能失败。

高盛打算买入其中的W公司，当时股价是30.5美元。

如果合并事宜谈妥的话，W公司的股价上涨可能3美元，

如果合并失败，W公司的股价有可能下跌6美元左右。

这相当于是对骰子上面的数字估值，接下来还要估一下每一面出现的可能性。

把合并成功的可能性定为大约85%，失败的可能性为15%。

接下来，我们计算一下期望值：股价可能上涨的幅度是3美元乘以85%，而下跌的风险是6美元乘以15%。

二者相加，该投资的期望值是每股1.65美元 。

该投资计划三个月内完成：

普通人看这个案例，可能会觉得满头雾水。

涨多少跌多少钱是猜的，涨跌的可能性也是猜的，这种计算有意义吗？

期望值的计算，提供了一个分析框架，用于面向不确定性未来的决策和下注。

对于股价可能的涨幅和跌幅，有赖于专业能力与经验；

对于交易是否可能完成，有赖于专业以及情报。

以上两件事情水平再高，也需要放在期望值计算的分析框架下，才能与不确定性共舞。

不管这次交易预测得多么准，结果都可能是出乎意料的，与期望值相去甚远。

就像扔骰子，期望值是3.5，但是你扔出一个6的可能性还是有1/6。

但是，假如你扔很多次，你就会很接近期望值。

所以，期望值的计算，提供的是一种“模糊的精确”，重复次数越多，就越精确。

04

尽管计算这么简单，期望值让很多专业人士都犯晕。

塔勒布就曾经嘲笑索罗斯曾经的搭档罗杰斯，说对他这样一个连期望值都弄不明白的家伙，赚的钱有点儿太多了。

似乎华尔街也有很多人不懂。塔勒布在一次投资研讨会说：“我相信下个星期市场略微上涨的概率很高，上涨概率大概70%。”但他却大量卖空标准普尔500指数期货，赌市场会下跌。

当时很多人不明白啥意思。他的意见是：市场上涨的可能性比较高（我看好后市），但最好是卖空（我看坏结果），因为万一市场下跌，它可能跌幅很大。

假使下个星期市场有70%的概率上涨，30%的概率下跌。但是如果上涨只会涨1%，下跌则可能跌10%。未来预期结果是：70%×1%+30%×（-10%）=-2.3%，因此应该赌跌，卖空股票盈利的机会更大。

让我们在回到本文开头的观点：

期望值未知的，是投机。

高盛的案例，看起来是期望值为正的投资。

塔勒布的下注，看起来像期望值未知（只是“我相信”）的投机。

那么赌博呢？

以美国的轮盘赌为例：

常用的轮盘上有38个数字，每一个数字被选中的概率都是相等的，也就是1/38。

你下注在某一个数字上，如果押中，赚相当于赌注35倍的奖金（赌注不包含在内），若没押中，你输掉赌注。

我们来算一下期望值，假如你每次押1块钱：

35×1/38-1×37/38，结果约等于-0.0526元。

也许你偶然会押中，本钱变成36倍，甚至押中了好几次，但是只要你持续玩儿下去，大数定律就会发挥作用，你会稳稳地输光所有本钱。

所以，这个世界上靠“稳定”的概率来赚钱的，也许只有赌场老板。

反过来，假如你是一个想追求稳定概率的赌徒，你会输得很稳定，穷得很稳定。

何止是赌徒，在现实中，为了虚幻的确定性，人们愿意做任何事情。

05

好了，假设我们都知道了“期望值”这个概念，也暂时假设我们对于涨幅跌幅以及对应的发生概率估算很靠谱，那么是不是就可以走在成为投资高手的路上了？

还是不行。

2016年，物理学家奥利.彼得斯和诺贝尔物理学奖得主默里.盖尔曼写了一篇关于遍历性的论文，里面有个例子：

有个玩硬币的赌博游戏，你投入1元，50%可以得到0.6元，50%可以得到1.5元。

根据期望值计算，一半可能性损失40%，一半可能性盈利50%，算下来数学期望是5%。

用流行的话说，这是大概率赚钱的事情，你可以大胆玩这个游戏。

不过，这个游戏有两种玩儿法，确切说，是有两种不同的下注方式：

方式a：你每次都拿1块钱去玩，假设你有无限多个1块钱，你可以一直玩下去，从长期来看你肯定是赚钱的，平均每把用5%的数学期望算是0.05元。

缺点是太慢，而且你必须有足够多的时间能玩下去。

方式b：拿出自己能拿出的最大的资金，然后投入进去。

后面这种玩儿法，就是所谓的All in。看起来极端，其实很多人都是这么干的，我自己也经历过，谁没年轻（蠢）过啊。

我们来做个简单的计算吧。

你本金一百万，第一把赢，第二把输，第三把再赢，如此持续下去。

直觉上看，100万本金，赢了是赚50万，输了是亏40万，为什么不能玩儿呢？

拿张纸，用中国当前幼儿园小班的数学能力计算一下：

100万 × (1+50%) × (1-40%) × (1+50%)(1-40%)......

一直这么玩儿下去，你会发现，没有几把就没钱了。

这难道不是绝大多数普通人做投资的现实吗？

韭菜自己被割起来更加无痛，没准儿还觉得是自己被割的时候姿势没摆好，天天继续勤学苦练，把辛辛苦苦的钱接着拿去All in下一个风口。

这里计算的关键，是算术平均值和几何平均值之间的差别。

假如你花100万买了一只基金，第一年涨了100%，第二年跌了50%。那么你的收益是多少？

按照算术平均值计算：

平均收益率=(第一年收益率+第二年收益率)/2=(100%-50%)/2 = 25%。

按照几何平均值计算：

年收益率假设是x，(1+x) × (1+x)=(1+100%) × (1-50%)=1，计算结果，x=0。

也就是说，按照几何平均数算，年回报率是零。实际就是如此。

这里用几何平均值计算出来的回报率，就是所谓“年化回报率”。

对比而言：

“年化回报率”（几何平均收益率）更准确地反应基金实际的历史收益情况；

算术平均收益率放大了投资的收益率。

下次买基金，记得问一下：

这只基金多久了？这个回报率是算术平均值还是几何平均值？